Kepler’s laws

Copernicus was met with rage from the church when he suggested in 1543, based on observations, that the planets were moving in circular orbits around a stationary sun. The idea that the sun was the center of the Universe, and not the Earth, was unheard of in a culture heavily influenced by the inherited teachings of the Roman Catholic Church. The findings of Copernicus ignited the heliocentric Copernican Revolution in Europe.

Figure 1: Many ancient and medieval cultures believed the stars and the planets rotated around a fixed Earth. The complex motions of the planets – which sometimes move against the perceived rotation of the rest of the sky (retrograde motion, shown in the photo) – led Renaissance astronomers to question this geocentric theory. These astronomers discovered the laws of orbital mechanics, transforming natural philosophy into the practice of science. Credits: Tunç Tezel.

Johannes Kepler, based on more accurate observations, corrected what Copernicus had found by stating that the orbits of the planets are not circular, but elliptic. That means that the Sun is not the center of the Solar System, but is located in one of the focal points of each of the planets ellipses. It was later, when Isaac Newton and Gottfried Leibniz discovered calculus, that it was shown mathematically that Kepler’s laws of planetary motion were shown to be correct.

Kepler stated three laws, now known as Kepler’s laws of planetary motion.

As already mentioned, fhe first law says that any satellite (artificial or natural) moves in an elliptical orbit around its central body. The central body is located in one of the focal points of the satellites ellipse, and the other focal point is empty.

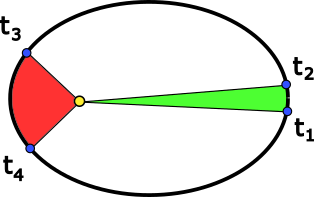
The second law states that the area speed is constant. The area speed is the area swept by the line between the central body and the satellite over a certain time span. In figure 2, two equi-sized sectors at different time coordinates $t_1, t_2$ and $t_3, t_4$ are marked with red and green. Since the size of the areas are equal, Kepler’s second law dictates that $t_2-t_1 = t_4-t_3$ . Hence, the orbital speed of the satellite must be high when the satellite is close to the central body, and lower when it is further away.

Figure 2: A satellite is orbiting a star. The red and the green areas are equal in size, so by Kepler’s second law, the satellite must use the same time between t1 and t2 as for t3 and t4. Illustrated by Andøya Space Education.

The third law states that for an orbiting satellite, the square of the period $T$ is proportional to the cube of the semi-major axis $a$ (see next section): $T^2 = \text{const} \cdot a^3$ . The constant depends upon the sum of the involved masses, but for a light satellite orbiting a much heavier central body the contribution from the satellite can be ignored. Thus, this constant is approximately equal for all (light) satellites orbiting a given body.

It is important to know that the Kepler orbits assume one central, stationary body with a large mass, and an orbiting satellite with a much smaller mass. Other effects, such as solar radiation pressure, atmospheric drag, gravitational influence from other planets and relativistic effects (which are crucial for an accurate calculation of the orbit of Mercury), are neglected. These approximations make the orbits easier to work with mathematically, but they also give reasonable predictions for many practical applications.

<< Previous page – Content – Next page >>

This article is part of a pre-course program used by Andøya Space Education in Fly a Rocket! and similar programs.