Nozzle

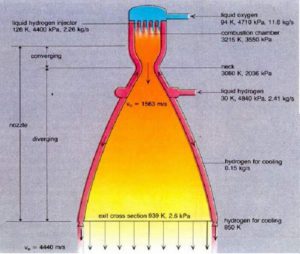
020520_102323_2 — Figure 1. Source: The Cambridge Encyclopaedia of Space.

When the propellant in a rocket engine burns, the warm combustion products are pressed out of the engine at high speeds. In order for the engine to gain as much speed as possible, the nozzle of the rocket engine should be shaped in a special way. The gases are pressed through a thin opening in the nozzle that first narrows and then widens, as seen in figure 1.

The gaseous combustion products may have a temperature of above $3000 \, ^\circ \text{C}$ and are pushed backwards at a violent speed. In order for the rocket to excert as high of a force as possible, it is important to give the combustion products the highest speed possible.

In this section we will discuss how the nozzle works and why it is shaped in this specific way.

The de Laval nozzle

The nozzle is an important part of any rocket motor. It converts high pressure and high temperature (with slow net velocity), inside the combustion chamber, into high velocity, but low pressure. In the combustion chamber the mixed propellant molecules have very high individual velocities, but their directions are largely random, i.e. pointing in all directions. This is what high pressure is. The nozzle helps align the movement of the molecules in the same direction. This means that it converts high pressures to high uniform velocity (and hence, high exhaust velocity). See figure 2. This is known as a converging-diverging nozzle (CD nozzle) or a de Laval nozzle (named after its Swedish inventor).

In figure 2, the CD nozzle is shown. For the CD nozzle, we have a version of Bernoulli’s equation given as

$\displaystyle \frac{\text{d}A}{A} = \left( M^2 - 1 \right) \frac{\text{d}v}{v},$

which tells us how the velocity $v$ changes with $\text{d}v$ through the nozzle as the sectional area $A$ of the nozzle changes with $\text{d}A$ . Here, $M = v/c$ is the Mach number, with $c$ being the speed of sound in the medium. At $M=1$ the net velocity of the molecules is at the so-called ‘sound barrier’.

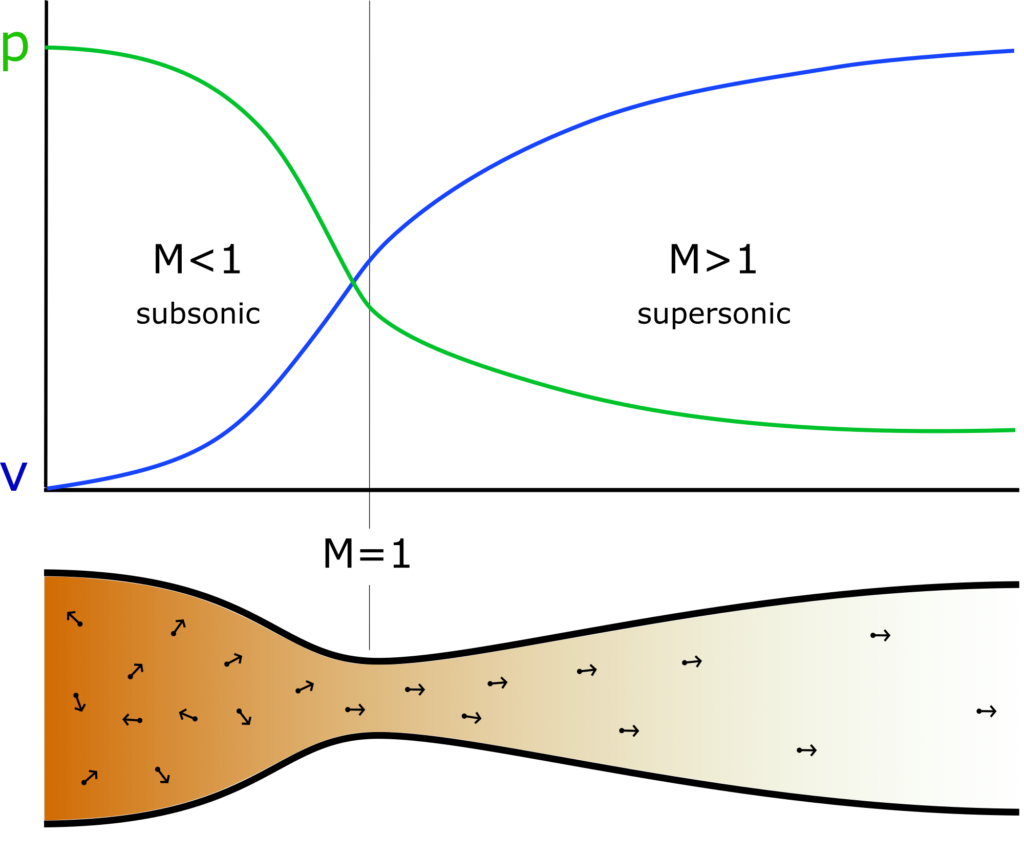
Figure 2: Schematic de Laval nozzle displaying the molecule movements, corresponding pressure and velocity curves throughout the converging subsonic and diverging supersonic crosssections. Illustrated by Andøya Space Education.

Let us assume that net velocity in the combustion chamber, shown on the lefthand-side of figure 2, is $M \ll 1$ (i.e. well below the speed of sound) and that thus we have a subsonic flow. Then $\displaystyle \left( M^2 - 1 \right) \frac{\text{d}v}{v},$ is negative, and as the sectional area decreases, i.e. when $\text{d}A < 0$ , the velocity has to increase, i.e. $\text{d}v > 0$ . This corresponds to our ‘normal’ expectations and means that the nozzle starts to converge. At the throat and into the diverging section, still assuming $M < 1$ , the velocity will decrease again ( $\text{d}v < 0$ ) while the sectional area increases ( $\text{d}A > 0$ ). Since the nozzle exit has a larger area than the entry towards the combustion chamber, the net velocity has actually decreased and we have gained nothing.

But, when looking at the equation, there is a trick we can do. Assuming that the throat sectional area is so small that we have reached $M = 1$ in the throat, we have a completely different case. In the combustion chamber, assuming $M < 1$ , the velocity will still increase with the decreasing area. It increases now to the point $M = 1$ at the throat. Looking at the equation for the divergent section of the nozzle, both sides must now have the same sign, since $M^2 -1 > 0$ . This means that just after the throat, where the velocity is slightly above the speed of sound, the velocity will actually increase with increasing sectional area. That is, when $\text{d}A > 0$ , we also have $\text{d}v > 0$ . This is very unintuitive, but we live in a world where humans never experience the direct effect of supersonic speeds. We have now gained high velocities at the cost of pressure.

The ideal nozzle design is when the pressure in the exhaust gas is equal to the ambient pressure. When this is true, all the velocity is pointing straight backwards from the nozzle and all the velocity is used to increase the velocity of the rocket. When this is not true, some of the energy is used to force the gas inwards or outwards perpendicular to the travelling directions, and this is energy which we cannot use to gain velocity for the rocket. Any specific CD nozzle is only ideal at a given height, since the exhaust pressure is constant while burning (from the design shape of the nozzle), but the ambient pressure is decreasing with increasing height. Hence the nozzle is only optimal at a given altitude, and designers need to tune their design according to its intended purpose, minimizing energy loss as much as possible.

<< Previous page – Content – Next page >>

This article is part of a pre-course program used by Andøya Space Education in Fly a Rocket! and similar programs.